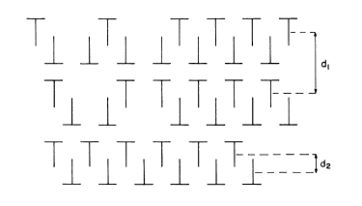
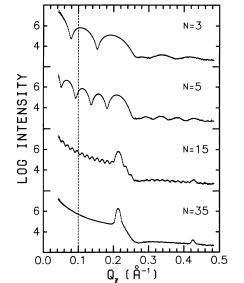
A model of x-ray diffraction for thin smectic-A liquid-crystal films is presented. The effect of the smectic-layer displacement fluctuations and correlations and the molecular form factor on the interlayer structure and the x-ray-diffraction pattern is discussed. In thin films the influence of the displacement-displacement correlation function on the x-ray-diffraction pattern is very small and can be neglected in the analysis of experimental data. On the other hand, both the displacement-fluctuation term (Debye-Waller factor) and molecular form factor produce strong measurable effects and so can be determined. We discuss the dependence of displacement fluctuations, calculated in the framework of the Landau–de Gennes model, on the smectic elastic constants and the smectic-vapor surface tension and show that these constants can be determined from the x-ray-diffraction pattern. The analysis of the hydrodynamic (collective) layer fluctuations and the individual molecular-motion fluctuations shows that the latter can be neglected in comparison to the former. The fluctuation amplitudes predicted by the model agree within 5% with the recent experimental measurements performed on smectic-I on –C films.

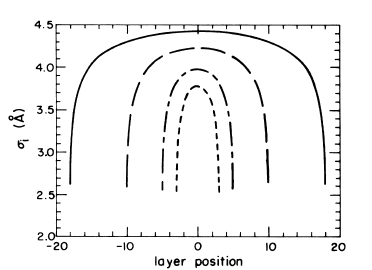
In thin smectic films the fluctuation amplitudes σ(r)=[〈$u^2$(r)〉${]}^{1/2}$ are only ∼4 Å compared with ∼8 Å in a macroscopic sample. The fluctuations are suppressed at the two free surfaces by the large surface tension, grow away from each surface, and have a parabolic profile near the center of the film. We argue that one of the reasons for surface freeezing in smectic liquid crystals is the quench of the layer fluctuations by the large surface tension. However, we also show that in systems with small surface tension the fluctuations at the surface are in fact larger than the ones in the interior of the system. The growth of the diffuse scattering, due to the displacement-displacement correlations, with the thickness of the smectic film is discussed and shown to evolve towards the structure predicted for large samples by Gunther, Imry, and Lajzerowicz [Phys. Rev. A 20, 1733 (1980)]. The model for the displacement layer fluctuations including the director as an independent variable is presented. Furthermore, the coupling between the layer fluctuations and the nematic order parameter in smectic liquid crystals is qualitatively discussed. It is argued that the compressional modes induce the nematic order-parameter fluctuations and that a large fluctuation profile may induce the smectic-A–smectic-C phase transition in thin films. Eventually in tilted smectic liquid crystals the layer fluctuation profile may induce a tilt profile. Finally, it is shown that the presented model can be applied to smectic systems other than smectic-A; we give explicit formulas for the x-ray-scattering intensity from the smectic-$A_d$ films and also calculate the fluctuations amplitudes for the stratified smectic-I on –C system.

We study two systems of hard biaxial molecules: hard spheroplatelets and hard ellipsoids, using the liquid-crystalline version of the smoothed density approximation (SDA). The first system is studied for all elongations of the spheroplatelet c, whereas the second only for c ⩽ 7. For both systems, we locate the line of Landau bicritical points at which a direct transition from the isotropic phase to the biaxial phase occurs. We find that the density of the isotropic phase at the Landau bicritical point is always higher than that at the isotropic-nematic transition in the limit of uniaxial molecules and the difference ranges from 10 to 30 per cent. For hard ellipsoids, we obtain a similar scaling behaviour at the Landau bicritical point as for spheroplatelets, i.e. b ∼c ^1/2, where b denotes the breadth of the ellipsoid.

Using the generalized Kirkwood-Buff formula for a surface tension we study the interfacial properties of liquid crystals. Surface tension, δ, is calculated for the dilute hard rod system in the sharp interface approximation as a function of a tilt angle, θ_t, measured from the normal to the flat interface. This function has a minimum at θ^eq_t corresponding to the preferred orientation of liquid crystal molecule at the nematic-isotropic interface and in our case θ^eq_t = 60°. We also argue that hard-core repulsion favours perpendicular alignment at the nematic free surface i.e θ_t=0°.

We present a density-functional theory, based on the smoothed density approximation, to study systems of hard rods with full translational and orientational freedom. For hard spherocylinders, we find both the nematic-isotropic and the nematic–smectic-A transition in a wide range of length-to-width ratios (L+D)/D. We locate the tricritical point for the nematic–smectic-A transition and also make some predictions about the nematic–smectic-A–smectic-B point. Finally, we calculate the nematic elastic constants. The predictions of our theory are compared with the results of computer simulations and other theories. We also make some comments about application of the theory to systems of hard ellipsoids of revolution and hard cylinders.

We analyze a system of hard parallel molecules that are composed of hard cylindrical cores and infinitely long and infinitely thin tails. We show that this system exhibits a continuous nematic–smectic-$A_d$ phase transition at zero packing fraction. The transition is studied in the framework of the virial expansion of the free energy. Keeping only the second virial coefficient in the expansion we find the transition at $B_2$ρ=1.80 and $d_1$/L=1.56, where the density ρ is measured in units of the second virial coefficient $B_2$, and the basic smectic period $d_1$ in units of the total length L of a molecule.

We study a system of hard parallel cylinders in the framework of the smoothed-density approximation (SDA). Using a bifurcation analysis, we argue that, apart from the nematic phase, smectic-A, solid (or crystalline smectic-B) and columnar phases should also occur in this system. We predict the following sequence of phase transitions: nematic-smectic-A at η* = η/η_cp = 0·31, smectic-A-solid (or smectic-B) at η* ≈ 0·59 and solid (or smectic-B)-columnar at η* ≈ 0·84, where η_cp = 0·9069 is the close-packing density. In our approach we cannot distinguish between a solid phase and a crystalline smectic-B phase.

X-ray diffraction has been used to study the interlayer structure of fluid freely suspended liquid-crystal films versus film thickness. The observed scattering is described extremely well by a simple interlayer density model based on predicted layer fluctuation ${\sigma }_i$ and tilt angle ${\phi }_i$ profiles. The diffraction data determine the individual ${\sigma }_i$’s to about ±0.1 Å, and the layer-fluctuation profiles calculated for the hydrodynamic fluctuations agree to this precision. The tilt profiles calculated using a simple elastic theory are also in excellent agreement with the data.

The smectic layer displacement fluctuation profile, σ(r)=〈$u^2$(r)${⟩}^{1/2}$, has been calculated for thin smectic-A films. In thin smectic-A films the calculated fluctuation amplitudes are only σ≊4 Å, compared to σ≊8 Å in a macroscopic sample. The fluctuations are suppressed at the two free surfaces by the surface tension, grow rapidly away from each surface, and have a parabolic profile near the center of the film. These results are in quantitative agreement (±0.1 Å) with recent x-ray measurements.

The theory of x-ray diffraction for smectic-A films is presented. The effect of the smectic layer fluctuations and correlations and the molecular form factor on the interlayer structure and the x-ray diffraction pattern is discussed. The application of the presented theory to smectic-C, smectic-I, smectic-A_d, and smectic-$A_2$ films is suggested.

We apply the smoothed-density approximation to study the nematic–smectic-A transition for the system of perfectly aligned hard spherocylinders. We find that the transition occurs for all length-to-width ratios L/D of a spherocylinder and is always continuous. The bifurcation analysis is applied to locate the transition. Our results are in reasonable agreement with those obtained in computer simulations

A new generalization of the Ornstein-Zernike equation for the functions describing equilibrium correlations between two groups of particles is proposed. The generalized direct correlation functions for two groups of particles are introduced, and the integral equations relating these functions to “full” correlations are derived. The derivation is based on diagrammatic analysis of the correlation functions. As an analogue of a cutting (nodal) vertex in the standard analysis leading to the Ornstein-Zernike equation we consider now a cutting set of vertices. Possible applications of the proposed formalism to the actual calculation of three- and four-particle equilibrium correlation functions are indicated.

Exact statistical mechanical sum rules for the pressure p and surface grand potential Θ _s of system of hard-rods near a hard wall are derived. The system is studied in the nonlocal version of Onsager low-density approximation. Θ _s , the equilibrium density and the nematic order parameter profiles at the bulk nematic-isotropic coexistence are calculated. The nonlocal approximation is shown to satisfy the pressure sum rule. From the behaviour of the profiles we conclude that the geometrical packing effects manifest themselves most strongly in the density profile and rather weakly in the order parameter profiles.

We apply the smoothed density approximation to study the nematic phase-isotropic phase transition (N-I) for the following systems: hard ellipsoids of revolution (HE), hard spherocylinders (HSC), and cylinders (HC). We find that the transition is very sensitive to the shape of the hard core modelling a liquid crystal molecule. In the case of HC, the nematic phase can exist in the whole range of elongations x, while for HE and HSC the nematic density at the transition exceeds the close packing density in some range of x, around x = 1. Also the dependence on x of the nematic order parameter, Q, the density, Δη, and entropy, ΔS, jumps at N–I transition is completely different for HC in comparison to HE and HSC.

Wetting phenomena on a sphere of radius R are studied in the context of the Sullivan model. Neither a first nor a continuous transition is found for finite R. Only in the strict limit of R→∞ a second-order transition appears. For temperatures T higher than the wetting temperature in a flat geometry, T^∞_w, the thickness l of the enhanced density layer, which forms on the surface of the sphere, is for large R proportional to In R.

A fluid of hard spherocylinders is studied in the Onsager model adapted to a nonuniform system. The interfacial properties at nematic-phase–isotropic-phase coexistence are considered. It is found that the angle between the director and the normal to the interface is approximately 60° and does not depend on the length-to-width ratio L/D of the spherocylinder. The nematic-phase–isotropic-phase surface tension, however, tends linearly to zero as D/L→0. It is also argued that the anisotropic hard-core repulsion favors the perpendicular alignment at the nematic free surface. The results concerning the tilt angle are in good agreement with experimental studies for nCB (n=5,6,7,8) [(4-n-alkyl-4’-cyano)biphenyl].