A flat, freely suspended film of smectic-A liquid crystal supports a pressure difference, Δp, across its two free surfaces. The size of its meniscus is about 10 μm, 2 orders of magnitude smaller than the capillary length, and its profile is predicted to be circular, in accordance with our measurement. The measurement of its radius of curvature gives Δp. We nucleate ex nihilo an elementary edge dislocation loop, and from its critical radius and growth dynamics (governed by Δp), we find the line tension (∼8×10⁻⁷dyn) and the mobility of an elementary edge dislocation (∼4×10−7cm²s/g).

We introduce a concept of topological disorder line for systems with ordered internal surfaces. At one side of the line the ordered structure exhibits strong topological fluctuations, accompanied by changes in the Euler characteristics. At the other side topological fluctuations are rare. In a system of oil-water-surfactant, in the lamellar phase, the crossover between two regimes is marked by the appearance of thin wormhole passages and their further proliferation. Close to the lamellar-microemulsion phase boundary thin wormhole passages merge leading to the formation of large channels between lamellas pierced with holes. The lamellar phase with many large “torus-like” passages strongly resembles the microemulsion phase. In order to illustrate these concepts we perform Monte Carlo simulations of the one scalar order parameter Landau–Ginzburg model of microemulsions. We show how the Euler characteristics can be effectively used in such simulations to identify different ordered phases and count the number of wormhole passages.

We present theoretical predictions of the distribution functions for ²H NMR bandshape for polymerized surfactant monolayers in triply periodic surfaces formed in ternary mixtures. We have calculated the distribution function for many triply-periodic structures of different topology, geometry, and symmetry. We have investigated applicability and usefulness of this new experimental technique to study the microstructures formed by surfactant molecules. The results presented in this paper can help experimentalists in better interpretation and analysis of nuclear magnetic resonance (NMR) bandshape experiments.

The lamellar phase between two parallel walls, in the water, oil, surfactant system, exhibits strong topological fluctuations. As we change the distance between the walls we observe the formation of two layers, then the microemulsion between two layers, and finally four layers. The transition is marked by the peaks in the average Euler characteristics and in its variance. The topological fluctuations may be responsible for attractive background force found in force apparatus measurements of the system.

We apply density functional theory to study the influence of polydispersity on the stability of columnar, smectic, and solid ordering in the solutions of rodlike macromolecules. For sufficiently large length polydispersity (standard deviation $\sigma >0.25$) a direct first-order nematic-columnar transition is found, while for smaller σ there is a continuous nematic-smectic and first-order smectic-columnar transition. The length distribution of macromolecules changes neither at the nematic-smectic nor at the nematic-columnar transition. In the binary mixtures the nematic-smectic transition is also continuous. Demixing in the smectic phase is preempted by transitions to solid or columnar phases.

A novel method is presented for generating periodic surfaces. Such periodic surfaces appear in all systems which are characterized by internal interfaces and which additionally exhibit ordering. One example are systems of AB diblock copolymers, where the internal interfaces are formed by the chemical bonds between the A and B blocks. In these systems at least two bicontinuous phases are formed: the ordered bicontinuous double diamond phase and the gyroid phase. In these phases the ordered domains of A monomers and B monomers are separated by a periodic interface of the same symmetry as the phases themselves. Here we present a novel method for the generation of such periodic surfaces based on the simple Landau‐Ginzburg model of microemulsions. We test the method on four known minimal periodic surfaces, find two new surfaces of cubic symmetry, and show how to obtain periodic surfaces of high genus and n‐tuply continuous phases (n > 2). So far only bicontinuous (n = 2) phases have been known. We point out that the Landau model used here should be generic for all systems characterized by internal interfaces, including the diblock copolymer systems.

In this paper we present a novel method for the generation of periodic embedded surfaces of nonpositive Gaussian curvature. The structures are related to the local minima of the scalar order parameter Landau-Ginzburg Hamiltonian for microemulsions. The method is used to generate six unknown surfaces of $\mathrm{Ia}\overline{3}d$ symmetric (gyroid) of genus 21, 53, 69, 109, 141, and 157 per unit cell. All of them but that of genus 21 are most likely the minimal surfaces. The Schoen-Luzzati gyroid minimal surface of genus 5 (per unit cell) is also obtained.

We analyse and simulate a two-dimensional Brownian multi-type particle system with death and branching (birth) depending on the position of particles of different types. The system is confined in a two-dimensional box, whose boundaries act as the sink of Brownian particles. The branching rate matches the death rate so that the total number of particles is kept constant. In the case of m types of particle in a rectangular box of size  and elongated shape  we observe that the stationary distribution of particles corresponds to the mth Laplacian eigenfunction. For smaller elongations a > b we find a configurational transition to a new limiting distribution. The ratio a/b for which the transition occurs is related to the value of the mth eigenvalue of the Laplacian with rectangular boundaries.

The polymer systems are discussed in the framework of the Landau‐Ginzburg model. The model is derived from the mesoscopic Edwards Hamiltonian via the conditional partition function. We discuss flexible, semiflexible and rigid polymers. The following systems are studied: polymer blends, flexible diblock and multi‐block copolymer melts, random copolymer melts, ring polymers, rigid‐flexible diblock copolymer melts, mixtures of copolymers and homopolymers and mixtures of liquid crystalline polymers. Three methods are used to study the systems: mean‐field model, self consistent one‐loop approximation and self consistent field theory. The following problems are studied and discussed: the phase diagrams, scattering intensities and correlation functions, single chain statistics and behavior of single chains close to critical points, fluctuations induced shift of phase boundaries. In particular we shall discuss shrinking of the polymer chains close to the critical point in polymer blends, size of the Ginzburg region in polymer blends and shift of the critical temperature. In the rigid‐flexible diblock copolymers we shall discuss the density nematic order parameter correlation function. The correlation functions in this system are found to oscillate with the characteristic period equal to the length of the rigid part of the diblock copolymer. The density and nematic order parameter measured along the given direction are anticorrelated. In the flexible diblock copolymer system we shall discuss various phases including the double diamond and gyroid structures. The single chain statistics in the disordered phase of a flexible diblock copolymer system is shown to deviate from the Gaussian statistics due to fluctuations. In the one loop approximation one shows that the diblock copolymer chain is stretched in the point where two incompatible blocks meet but also that each block shrinks close to the microphase separation transition. The stretching outweights shrinking and the net result is the increase of the radius of gyration above the Gaussian value. Certain properties of homopolymer/copolymer systems are discussed. Diblock copolymers solubilize two incompatible homopolymers by forming a monolayer interface between them. The interface has a positive saddle splay modulus which means that the interfaces in the disordered phase should be characterized by a negative Gaussian curvature. We also show that in such a mixture the Lifshitz tricritical point is encountered. The properties of this unusual point are presented. The Lifshitz, equimaxima and disorder lines are shown to provide a useful tool for studying local ordering in polymer mixtures. In the liquid crystalline mixtures the isotropic nematic phase transition is discussed. We concentrate on static, equilibrium properties of the polymer systems.

We present a method for the generation of periodic embedded surfaces of nonpositive Gaussian curvature and multiply continuous phases. The structures are related to the local minima of the scalar order parameter Landau-Ginzburg Hamiltonian for microemulsions. In the bicontinuous structure the single surface separates the volume into two disjoint subvolumes. In some of our phases (multiply continuous) there is more than one periodic surface that disconnects the volume into three or more disjoint subvolumes. We show that some of these surfaces are triply periodic minimal surfaces. We have generated known minimal surfaces (e.g., Schwarz primitive P, diamond D, and Schoen-Luzatti gyroid G and many surfaces of high genus. We speculate that the structure of microemulsion can be related to the high-genus gyroid structures, since the high-genus surfaces were most easily generated in the phase diagram close to the microemulsion stability region. We study in detail the geometrical characteristics of these phases, such as genus per unit cell, surface area per unit volume, and volume fraction occupied by oil or water in such a structure. Our discovery calls for new experimental techniques, which could be used to discern between bicontinuous and multiply continuous structures. We observe that multiply continuous structures are most easily generated close to the water-oil coexistence region.

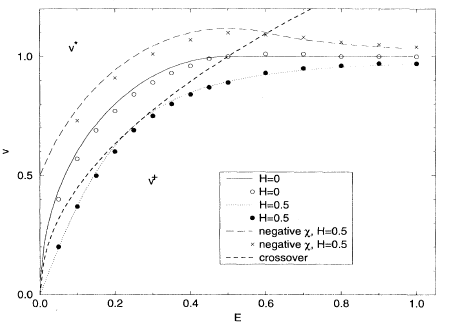
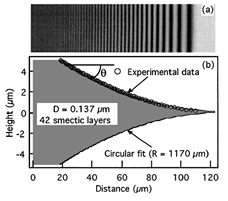
Dislocations in soft condensed matter systems such as lamellar systems of polymers, liquid crystals and ternary mixtures of oil, water and surfactant (amphiphilic systems) are described in the framework of continuum elastic theory. These systems are the subject of studies of physics, chemistry and biology. They also find applications in industry. Here we will discuss in detail the influence of dislocations on the bulk and surface properties of these lamellar phases. Especially the latter properties have only been recently studied in detail. We will present the experimental evidence of the existence of screw and edge dislocations in the systems and study their static properties such as: energy, line tension and core structure. Next we will show how the surface influences the equilibrium position of dislocations in the system. We will give the theoretical predictions and present the experimental results on thin copolymer films, free standing films of liquid crystals and smectic droplets shapes. In semi-infinite lamellar systems characterized by small surface tension the dislocation is stabilized at a finite distance, h_eq, from the surface, due to the surface bending elastic constant, K_s (for zero surface tension h_eq≈K_s/2K, where K is the bulk bending elastic constant). For large surface tension the edge dislocations are strongly repelled by the surface and the equilibrium location for finite symmetric systems such as free standing liquid crystal films shifts towards the center of the system. The surface is deformed by dislocations. These deformations are known as edge profiles. They will be discussed for finite systems with small and large surface tension. Surface deformations induce elastic interactions between edge dislocations, which decay exponentially with distance with decay length proportional to  where D is the size of the system normal to lamellas. Two screw dislocations in finite system interact with the logarithmic potential, which is proportional to the surface tension and inversly proportional to D. The surface induced elastic interactions will be compared to, well-known, bulk deformation induced interactions. A new phenonenon discussed in our paper is the fluctuations induced interactions between edge dislocations, which follows from the Helfrich mechanism for flexible objects. At suitable conditions, edge dislocations can undergo an unbinding transition. Also a single dislocation loop can undergo an unbinding transition. We will calculate the properties of the loop inside finite system and discuss in particular the unbinding transition in freely suspended smectic films. We shall also compute the equilibrium size of the loop contained between two hard walls. Finally we will discuss the dynamical bulk properties of dislocations such as: mobility (climb and glide), permeation, and helical instability of screw dislocations. Lubrication theory will also be discussed.

We discuss the front propagation in ferroelectric chiral smectic liquid crystals (Sm-$C^{*}$) subjected to electric and magnetic fields that are applied parallel to smectic layers. The reversal of the electric field induces the motion of domain walls or fronts that propagate into either an unstable or metastable state. In both regimes, the front velocity is calculted exactly. Depending on the field, the speed of a front propagating into the unstable state is given either by the so-called linear marginal-stability velocity or by the nonlinear marginal-stability expression. The crossover between these two regimes can be tuned by a magnetic field. The influence of initial conditions on the velocity selection problem can also be studied in such experiments. Sm-$C^{*}$ therefore offers a unique opportunity to study different aspects of front propagation in an experimental system.

The electric field applied perpendicularly to smectic layers breaks the rotational symmetry of the system. Consequently, the elastic energy associated with distortions induced by an edge dislocation diverges logarithmically with the size of the system. In freely suspended smectic films the dislocations in the absence of the electric field are located exactly in the middle of the film. The electric field, E, above a certain critical value, , can shift them towards the surface. This critical field (in Gauss cgs units) is given by the following approximate formula . Here, B and K are smectic elastic constants,  is the surface tension, N is the number of smectic layers and  is the dielectric anisotropy. The constant  and . Additionally, we assumed that , where d is the smectic period. This formula is valid for  and N>12. For smaller values of the surface tension and large N the linear relation between  and  breaks down, since eventually for  and ,  approaches 0. The equilibrium location of a dislocation in the smectic film, , equals NdG(x), where  and G(x) is a function independent of the film thickness (for N>12) and of the value of the surface tension.

We study two-dimensional Brownian motion in an ordered periodic system of linear reflecting barriers using the sampling method and conformal transformations. We calculate the effective diffusivity for the Brownian particle. When the periods are fixed but the length of the barrier goes to zero, the effective diffusivity in the direction perpendicular to the barriers differs from the standard one by a term of order epsilon ² where epsilon is the length of a barrier.

A Comment on the Letter by F. S. Bates et al., Phys. Rev. Lett. 65, 1893 (1990).