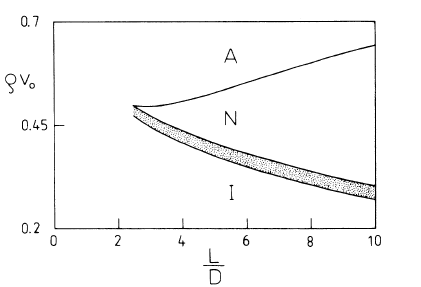
A system of hard spherocylinders near an impenetrable wall is studied in the low-density Onsager approximation. Using a simple local approximation for the one-particle distribution function, we show that the preferred orientation of the nematic director is parallel to the wall. The density and order-parameter profiles are calculated. The nematic main order parameter Q is enhanced near the wall even though the density is reduced. The wall-induced biaxiality P is small in the interfacial region. We find that wetting by the nematic phase should occur at the nematic-isotropic coexistence.

A density-functional theory, based on the smoothed density approximation, is presented in order to study phase transitions in systems of hard spherocylinders with full translational and orientational degrees of freedom. We find both the nematic-isotropic and the $nematic-Smectic-A$ phase transition in a wide range of length-to-width ratios $\frac{L}{D}$. The predictions of our theory are in good agreement with results of computer simulations and we recover Onsager’s limit of $\frac{L}{D}\to \infty$. We also make some comments about application of the theory to systems of hard ellipsoids.

We study a system of hard elongated molecules near a hard wall, placed in a strong bulk ordering field. The field fixes the tilt angle ϑ _t and increases the order parameter Q. We show that in the case of perfect alignment (Q = 1) the nematic-wall surface tension (γ) does not have the usual form of a polynomial in cos² ϑ _t . Using a simple local approximation for the one-particle distribution function we find an analytical expression for γ(ϑ _t ) for the system of hard cylinders and also calculate γ(ϑ _t ) numerically for the system of hard spherocylinders.

It is shown in the framework of the Cahn model [J. Chem. Phys. 66, 3667 (1977)] that the wetting layer, which forms on a spherical surface, always has a finite thickness $l\sim \ln R$ where $R$ is the radius of a sphere. The temperature $T_w$ of a first-order wetting transition is higher in a spherical geometry than in a flat one. The shift of the transition temperature $T_w$ is proportional to $\frac{\ln \mathrm{R/}}{R}$ for large $R$.