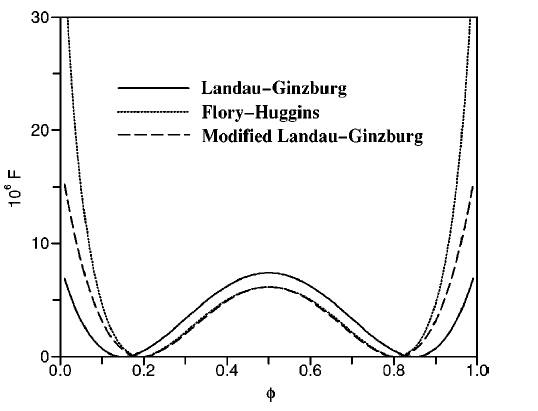
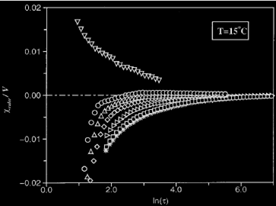
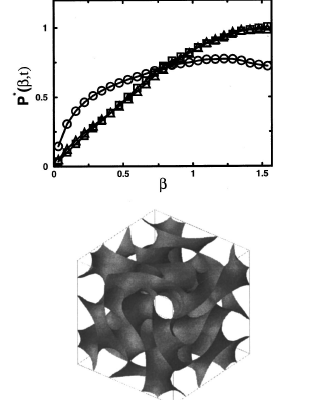
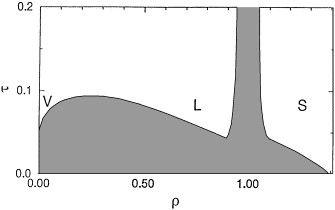
We briefly present the Kauzmann entropy crisis and show that it may have a simple explanation in terms of the entropy-driven phase transitions. We discuss in a pedagogical manner why the enthalpy change at the freezing transition is positive even for a hard sphere fluid, despite the fact that the transition is driven by the increase of the entropy. We use this observation to explain qualitatively the Kauzmann entropy crisis.

We have investigated the intermediate scaling regime in the phase ordering/separating kinetics of the three-dimensional system of the non-conserved scalar order parameter. It is demonstrated that the observed scaling behavior can be described in terms of two length scales L_H(t) ∼ t^2/5 and L_K(t) ∼ t^3/10. The quantity L_H(t) is related to the geometrical properties of the phase interface and describes time evolution of the characteristic domain size, surface area, and the mean curvature. The second length scale, L)K(t), determining the Gaussian curvature and the Euler characteristic, can be regarded as the topological measure of the phase interface. Also, we have shown that the existence of the two length scales has a simple physical interpretation and is related to the domains-necks decoupling process observed in the intermediate regime.

We present a simple numerical analysis of the diffusion on a curved surface given by the equation φ(r)=0 in a finite domain D⊂R3. The first non-vanishing eigenvalue of the Beltrami–Laplace operator with the reflecting boundary conditions is determined in our simulations for the P, D, G, S, S1 and I-WP, nodal periodic surfaces, where D is their respective cubic unit cell. We observe that the first eigenvalue for the surfaces of simple topology (P,D,G,I-WP) is smaller than for the surfaces of complex topology (S,S1).

We investigate the number N of molecules needed to perform independent diffusion in order to achieve bonding of a single molecule to a specific site in time $t_0.$ For a certain range of values of $t_0,$ an increase from N to kN molecules $(k>1)$ results in the decrease of search time from $t_0$ to $t_0/k.$ In this regime, increasing the number of molecules is an effective way of speeding up the search process. However when $N>~N_0$ (optimal number of N) the reduction of time from $t_0$ to $t_0/k$ can be achieved only by an exponentially large increase in the number of molecules [from N to $N\exp \left(\mathrm{ck}\right)$ for some $c>0].$

We compute scattering patterns for six triply periodic minimal surfaces formed in oil/surfactant/water solutions: Three surfaces of a simple topology, Schwarz P $\left(Im3¯m\right),$ Schwarz D–diamond $\left(Pn3¯m\right),$ and Schoen G–gyroid $\left(Ia3¯d\right),$ and three surfaces of a complex topology, SCN1 $\left(Im3¯m\right),$ CD $\left(Pn3¯m\right),$ and GX6 $\left(Ia3¯d\right).$ We show that in the case of the complex structures, scattering intensity is shifted towards the higher $\mathrm{hkl}$ peaks. This might cause their misidentification and wrong estimates about the cell size of the structure.

In order to activate a gene in a DNA molecule a specific protein (transcription factor) has to bind to the promoter of the gene. We formulate and partially answer the following question: how much time does a transcription factor, which activates a given gene, need in order to find this gene inside the nucleus of a cell? The estimate based on the simplest model of diffusion gives a very long time of days. We discuss various mechanisms by which the time can be reduced to seconds, in particular, the reduction of dimensionality, in which diffusion takes place, from three-dimensional space to two-dimensional space. The potential needed to keep the diffusing particle in 2D (i.e, at the surface of size L² in a volume of size L³) should scale as U∼kBTlnL. For aL=1μm and a target size a=10 Å we find U=8k_BT, i.e., it is a potential strength of the order of the strength of ionic interactions in water.

The spinodal decomposition of the homopolymer blends has been studied by the numerical integration of the Cahn–Hilliard–Cook equation. We have investigated the time evolution of the morphological measures that characterize quantitatively the interface in the system. For symmetric blends we have found that the Euler characteristic of the interface is negative and increases with time as τ0.75 (connectivity of the domains decreases) regardless of the final quench temperature. The homogeneity index of the interface is constant in this case. This suggests that at the level of the integral geometry quantities (Minkowski functionals), the dynamic scaling hypothesis holds for the evolution of the interface morphology in quenched critical systems. The nonuniversal morphological evolution of the asymmetric blends have been studied. Also, we have shown that the thermal fluctuations can modify significantly the curvature distribution.

Ordered phases formed by surfactants in water solutions, and used in technological processes as templates for the synthesis of mesoporous materials, exhibit topological fluctuations. From the results of the Monte Carlo simulations of the lamellar phase we have established a relation between topological fluctuations and the behavior of the off-specular scattering intensity. We have defined the topological Lifshitz line. At this line the peak position in the off-specular scattering intensity moves from the zero (lamellar phase with fixed topology) to the nonzero value of the scattering wave vector (lamellar phase with fluctuating topology).

The spinodal decomposition of a binary mixture has been studied within several mesoscopic models. It has been found that the form of the equilibrium free energy has a crucial effect on the morphological development in asymmetric blends. We have shown that the principal quantity that determines the topology of the interface (and type of morphology) is the equilibrium minority phase volume fraction, while the transition from bicontinuous to droplet morphology can be treated as a percolation. The concentration dependence of the square gradient coefficient attributed for the Flory-Huggins–de Gennes free energy has no significant influences on the average domain growth, but can be distinguished experimentally from its constant-coefficient alternative by measuring the maximum wave vector of the scattering intensity as a function of the minority phase volume fraction for spinodally decomposing asymmetric blends. The concentration dependence of the Onsager coefficient has the weak, systematic effect of slowing down the morphological development. The local shape of the interface is not affected considerably by the concentration dependence of the square gradient and Onsager coefficient.