Facebook Youtube

Publications

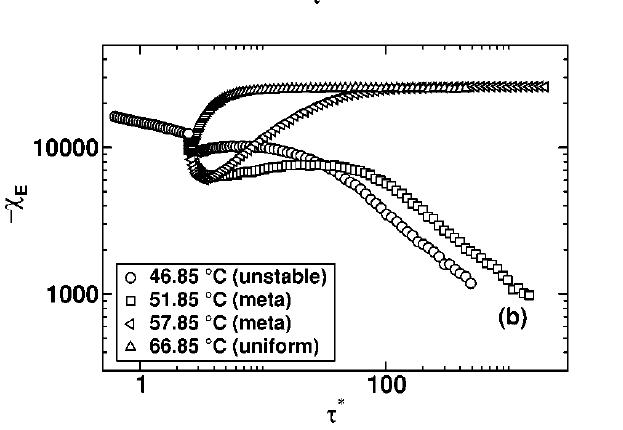
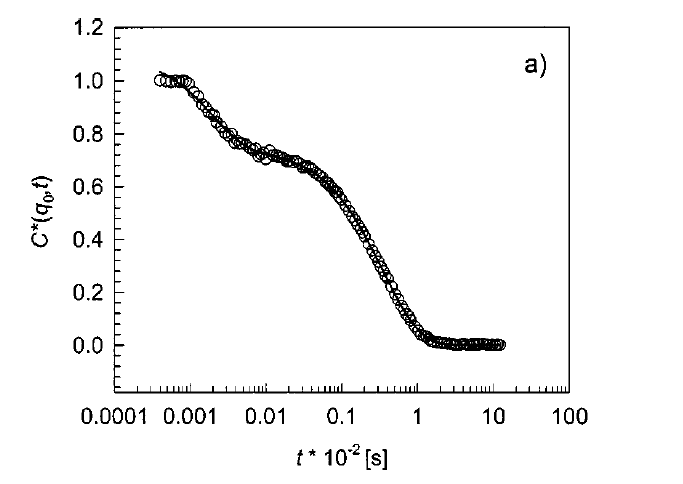
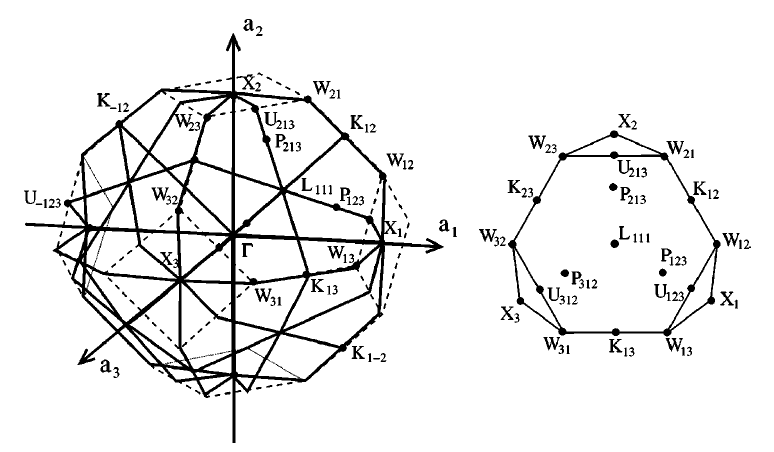
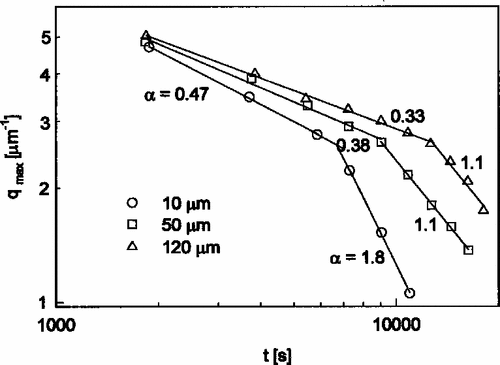
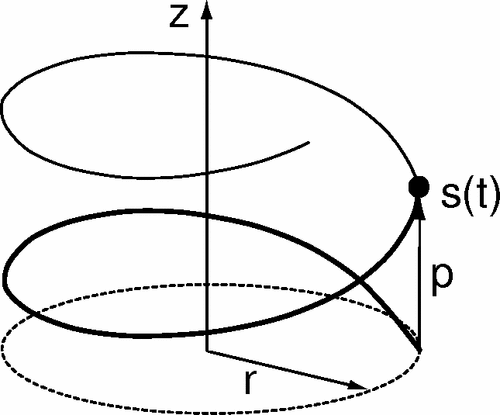
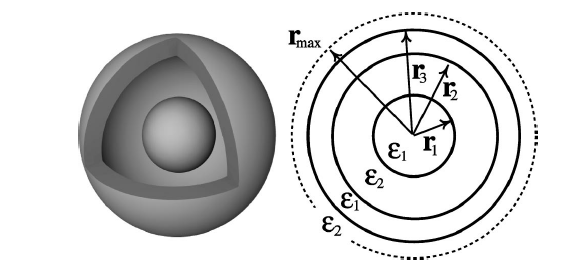
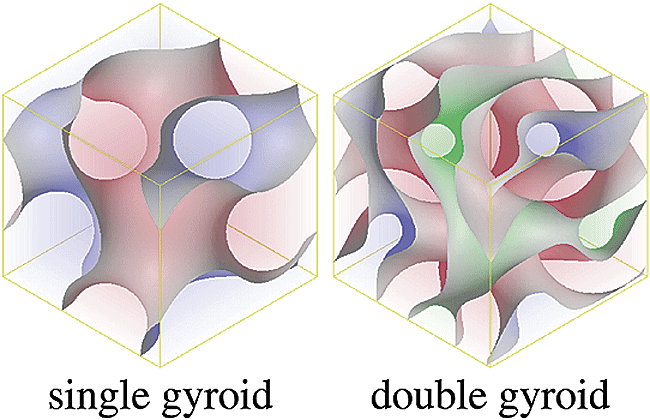
Some features of soft matter systems

R. Hołyst

Soft Matter, 2005,1, 329-333

Pierre Gilles de Gennes was awarded a Nobel prize in physics “for discovering that methods developed for studying order phenomena in simple systems can be generalized to more complex forms of matter, in particular to liquid crystals and polymers”. Thanks to his works “soft matter” became a new legitimate discipline in physics. Soft matter includes a vast range of materials, which cannot be classified as simple liquids or solids. Many soft matter systems exhibit partially broken translational and/or rotational symmetry. In others we observe mesoscopic self-assembling into supramolecular structures leading to viscoelastic behavior. The partial ordering with viscoelastic properties, topological and geometrical complexity, and long relaxations associated with broken symmetries and/or supramolecular assembling are the main features of these systems. Among them we find liquid crystals, gels, biological membranes, colloidal suspensions, polymer solutions and polymer melts and blends, surfactant solutions etc. Typical models used in soft matter theory are based on statistical mechanics and classical thermodynamics, supplemented by the theory of elasticity, hydrodynamics and thermodynamics of irreversible processes and also some elements of the field theory. In this short overview I would like to discuss three theoretical issues related to soft matter systems: interactions, the role of the entropy, and finally the order parameter description.

Minimization of the Renyi entropy production in the stationary states of the Brownian process with matched death and birth rates

O. Cybulski, V. Babin and R. Hołyst

Phys. Rev. E 2004, 69, 016110

We analyze the Fleming-Viot process. The system is confined in a box, whose boundaries act as a sink of Brownian particles. The death rate at the boundaries is matched by the branching (birth) rate in the system and thus the number of particles is kept constant. We show that such a process is described by the Renyi entropy whose production is minimized in the stationary state. The entropy production in this process is a monotonically decreasing function of time irrespective of the initial conditions. The first Laplacian eigenvalue is shown to be equal to the Renyi entropy production in the stationary state. As an example we simulate the process in a two-dimensional box.

The unphysical pinning of the domain growth during the separation of homopolymer blends near the spinodal

M. Fiałkowski and R. Hołyst

J. Chem. Phys. 2004, 120, 5802

We simulate model B of mesoscopic dynamic with the Flory–Huggins free energy for the homopolymer blend. We concentrate the study on the rescaling of the spatial coordinates in the model. We show that the commonly used rescaling of the spatial coordinates, by the function vanishing at the spinodal, leads to the unphysical freezing of the domains. We study the evolution of the system in two different processes: One is the growth process induced by the temperature quench to the metastable or unstable region of the phase diagram and the second is the quench-jump process in which we first allow the system to separate below the spinodal and next heat it up below or above the spinodal. The proper rescaling avoiding the unphysical pinning of the domain growth at the spinodal is proposed.

Absorption of Mercury in Gold Films and Its Further Desorption:  Quantitative Morphological Study of the Surface Patterns

M. Fiałkowski, P. Grzeszczak, R. Nowakowski and R. Hołyst

J. Phys. Chem. B 2004, 108, 16, 5026–5030

A thin film of Au exposed to mercury vapor disrupts forming separated domains of AuHg amalgam. After evaporation of Hg at high temperature Au islands are formed and the domain pattern changes. A detailed quantitative morphological analysis and comparison of two types of surface patterns before and after the evaporation of Hg is performed. We have found that during the evaporation of Hg at high temperature the islands decrease their sizes and their shapes become more circular. The domain pattern formed by the amalgam domains is found to be characterized by one length scale. After the removal of mercury the characteristic length scale vanishes and the structure function takes the shape typical for the random droplet morphologies.

Relaxation processes in mixtures of liquid crystals and polymers near phase boundaries and during phase separation

E. Freyssingeas, M. Graca, S.A. Wieczorek and R. Hołyst

J. Chem. Phys. 2004, 120, 8277

We present experimental studies of the relaxation of concentration fluctuations in a semidilute solution of polystyrene (PS) (30% by weight) in 4-cyano-4′4′–n-octyl-biphenyl (8CB) (70% by weight) using the photon correlation spectroscopy (PCS). In the homogeneous phase there are two modes of relaxation. The slow one (typical time scale is τs=0.001 s)τs=0.001 s) is due to the diffusion of polymer chains (of molecular mass 65 000) in the LC matrix (of molecular mass 290), while the fast one has the time scale of the order of τf≈0.00001 s.τf≈0.00001 s. The amplitude of the fast mode is much weaker than the one for the slow mode. Moreover it does not depend on the scattering wave vector, q. The value of the diffusion coefficient, Dc=1/(τsq2)Dc=1/(τsq2) for the slow mode decreases with temperature according to the Arhenius law until we reach the coexistence curve. Its value close to the coexistence is Dc=4×105 nm2/sDc=4×105 nm2/s and the activation energy in the homogeneous mixture is Ec=127 kJ/mol.Ec=127 kJ/mol. If we gradually undercool the mixture below the coexistence into the metastable two-phase region without inducing the phase separation we find unexpectedly that DcDc does not change with temperature even 4° below the coexistence curve. The characteristic time of the fast mode does not depend on the scattering wave vector indicating that it is related to the transient gel structure. We have shown that it is possible to measure the short time relaxation of concentration fluctuations during the phase separation in the mixture. At low temperature close to the isotropic–nematic phase transition we have observed that the relaxation is well separated in time from the typical time of the domain growth. This relaxation mode is characterized by the large diffusion coefficient D=2×108 nm2/s.D=2×108 nm2/s. The mode probably comes from the coupling between the orientational dynamics of liquid crystals and the transient gel structure of polymers.

A Morphological Study of the Formation of PdHx on Thin Palladium Films

M. Fiałkowski, R. Nowakowski and R. Hołyst

J. Phys. Chem. B 2004, 108, 22, 7373–7376

We propose a mechanism for the creation of the two-dimensional ridge pattern morphology during the formation of palladium hydride on the surface of thin palladium films at 298 K. Expressions for the distribution of domain areas and circumferences, derived from the maximum entropy principle, are in very good agreement with experiment.

Liquids with internal surfaces at and out of equilibrium: the homogeneity index

M. Fiałkowski, P. Garstecki and R. Hołyst

Journal of Molecular Liquids 2004,112, 1–2, 29-35

In this article, we discuss the application of the homogeneity index to the study of the morphology of the binary mixtures (two homopolymers) undergoing phase separation below the convolute (critical) point. The homogeneity index is a measure of how homogeneous, in terms of the local curvatures, is the interface, which is formed inside the system in the process of phase separation. In this article, we will compare the value of the homogeneity index for the phase separating binary mixture with the one for magnetic systems undergoing phase ordering and also to the homogeneity index known for various bicontinuous phases observed at equilibrium in the mixtures of surfactant-water systems. We will show that the homogeneity index is probably the best tool (most sensitive) for the study of the dynamic scaling in the ordering or phase separating systems.

Percolation-to-droplets transition during spinodal decomposition in polymer blends, morphology analysis

I. Demyanchuk, S. A. Wieczorek and R. Hołyst

J. Chem. Phys. 2004, 121, 1141

Phase separation kinetics of the off-critical mixture of polystyrene and poly(methylphenylsiloxane) is studied by the time-resolved light scattering and optical microscopy. The results from the light scattering experiments are correlated with the images obtained by the optical microscopic observation in order to find characteristic features of the scattering intensity during the percolation-to-droplets morphology transition. At the beginning of the spinodal decomposition process only a bicontinuous network is present in the system and the light scattering intensity has only one peak. The network coarsens and at the same time small droplets appear in the system resulting in a growth of the scattering intensity at very small wave vectors. When the large network starts to break up into disjoint elongated domains a second peak in the scattering intensity appears. Finally, both peaks merge into a single peak at zero wave vector, indicating a complete transformation of elongated domains into spherical droplets of variable sizes. The comparison of the direct microscopic observations with the light scattering spectra shows that the process of breaking up of the bicontinuous network starts when the growth of the first peak, corresponding to the bicontinuous pattern, becomes very slow (essentially pinned down).

Photonic properties of an inverted face centered cubic opal under stretch and shear

V. Babin, P. Garstecki and R. Hołyst

Appl. Phys. Lett. 2003, 82, 1553

We present the results of numerical calculations of the dispersion relations for an inverted fcc opal structure subjected to a stretch and shear. We find that shearing of the crystal only lowers the gap width and slightly changes the midgap frequency. Interestingly, that in a large range of stretch amplitudes (up to 10%) the gap width is preserved and even slightly enhanced. The midgap frequency depends almost linearly on the stretch amplitude allowing for tuning an inverted fcc opal structure to a desired operational frequency. This last property may be important for the manufacturing process.

Polymer Domain Growth in Ordered Liquid Crystalline Matrices

M. Graca, S. A. Wieczorek and R. Hołyst

Phys. Rev. Lett. 2003, 90, 115504

The growth of polymer domains in the isotropic, nematic, and smectic matrices is studied by the light scattering. In the smectic and isotropic matrices the growth is diffusive, and in the nematic matrix it is influenced by the elastic forces. The scaling is obeyed. A crossover to the wetting fast-mode hydrodynamic regime is also observed at long times. In order to perform these measurements we had to eliminate the multiple scattering of light.

Comment on “Tracer Diffusion in a Dislocated Lamellar System”

D. Constantin and R. Hołyst

Phys. Rev. Lett. 2003, 91, 039801

A Comment on the Letter by Victor Gurarie and Alexander E. Lobkovsky, Phys. Rev. Lett. 88, 178301 (2002). The authors of the Letter offer a Reply.

Growth of Polystyrene Domains in Isotropic, Nematic and Smectic Phase of 8CB Liquid Crystal

M. Graca, S. A. Wieczorek, and R. Hołyst

Macromolecules 2003, 36, 18, 6903–6913

A small-angle light-scattering (SALS) technique is performed to investigate the phase separation in the films of flexible polymer (polystyrene, PS) mixed with low molecular weight thermotropic liquid crystal LC (4-cyano-4‘-n-octylbiphenyl, 8CB). The growth of isotropic (polymer) domains is studied in both isotropic and anisotropic (nematic or smectic phase) LC matrices, as a function of time, film thickness, and film composition. The size of the domains, L(t), grows algebraically with time as L(t) ∼ tβ. For 70/30 wt % of 8CB/PS, we found the diffusion growth in isotropic (β = 0.25) and smectic (β = 0.28) matrices, independent of the film thickness. In the nematic matrix, β changes from 0.33 to 0.47 as we change the thickness of the sample from 120 to 10 μm. We think that the change of β is due to the attractive forces between the polymer domains which follow from the elastic deformations of the nematic matrix caused by the glass surfaces and polymer domains. In every matrix and for different thicknesses of a sample, scaling is observed in this growth regime. At longer times, there is a crossover from the diffusion growth to the hydrodynamic fast-mode growth, characteristic for systems in which one of the components wets the confining walls. In this regime, we do not observe the scaling; i.e., there is more than one characteristic length scale in the system, and β ranges from 1 to 3/2. Considering extremely viscous systems (50/50 wt % of 8CB/PS), we also find the diffusion growth but with smaller exponent β < 0.2. In this case, we observe two peaks in the scattering intensity S(q,t). One of them is the surface and one the bulk peak. For systems with small amount of a polymer (90/10 wt % of 8CB/PS), the process of growth is very fast, and β = 0.4. In this case, the bulk peak is very quickly covered by the peak coming from the growth of the domains at the surface. To perform the measurements in anisotropic LC systems, we had to eliminate the multiple scattering of light coming from the large difference in ordinary and extraordinary refractive indexes of LC.

Multiple photonic band gaps in the structures composed of core-shell particles

V. Babin, P. Garstecki and R. Hołyst

Journal of Applied Physics 2004, 94, 4244

We present a detailed study of the full photonic band gaps for the spherical multilayered core-shell particles arranged in bcc, fcc, and diamond fcc lattices. We find that layered structure of the particles does not lead to an increase of the gap width in case of the fcc arrangement. On the other hand full photonic band gap opens up for the bcc lattice composed of such particles. The most promising is the diamond fcc arrangement. For such ordering of core particles covered by a thin shell we find three reasonably wide gaps.

Scattering patterns of multiply continuous cubic phases in block copolymers. II. Application to various triply periodic Architectures

P. Garstecki and R. Hołyst

Macromolecules 2003, 36, 24, 9191–9198

The model for the scattering amplitudes is applied to a quantitative analysis of the scattering spectra of the n-block copolymer systems. The method allows interpretation of the X-ray diffraction patterns in systems of the multiblock copolymers forming multiply continuous triply periodic structures (MCTPS). We give simple formulas for the scattering intensity for structures of different topology and symmetry appearing in block copolymers. The straightforward fitting procedure presented in this article allows determination of the multicontinuous architecture adopted by a multiblock copolymer system, the volume fractions of the continuous domains and the width of the interdomain intefaces. The model is robust, i.e., applicable to n-block linear copolymers, and should be helpful in the quantitative analysis of the experimental data.

Scattering Patterns of Multiply Continuous Cubic Phases in Block Copolymers. I. The Model

P. Garstecki and R. Hołyst

Macromolecules 2003, 36, 24, 9181–9190

The X-ray scattering amplitudes are given for the multicontinuous P, D, G, and I-WP cubic phases formed in block copolymer systems. The formulas can be used to retrieve the scattering amplitudes for an arbitrary n-block copolymer system adopting one of the above multiply continuous triply periodic structures (MCTPS).

(+48) 22 343-31-23

softmatter@ichf.edu.pl

Kasprzaka 44/52, 01-224 Warsaw, Poland