Three-dimensional space partition based on the first Laplacian eigenvalues in cells
O. Cybulski and R. Hołyst
Phys. Rev. E 2008, 77, 056101
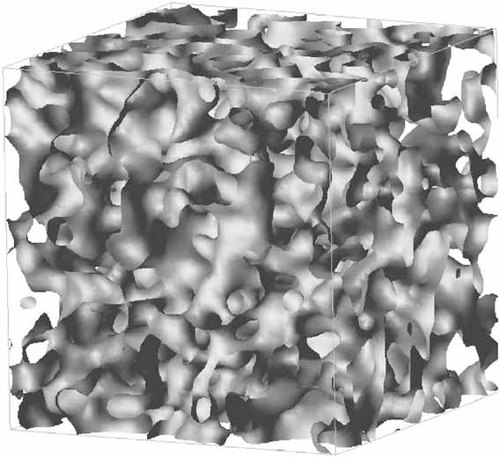
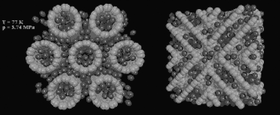
We determine a partition of three-dimensional space into cells by minimization of the sum of the first Laplacian eigenvalues over the cells. This partitioning scheme emerges as a stationary state of a reaction-diffusion process taking place in a system of n different species which mutually annihilate, and simultaneously are duplicated in an autocatalytic reaction, so that the number of particles is kept constant and equal for each species. The system is considered in the limit of strong reactivity, so that the species separate each other into cells with well-defined, sharp boundaries. For a given n and fixed sizes of a periodic simulation box, this partition minimizes the aforementioned sum of eigenvalues. Further minimization is done by changing n and the side ratio of the periodic box. The global minimum is obtained for the structure with A15 symmetry, similar to the Weaire-Phelan foam. Depending on n and the side ratio, there are also many local minima, in particular: hcp (hexagonal close packed), fcc (face centered cubic), the Kelvin structure, and Frank-Kasper sigma phase.