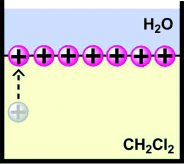

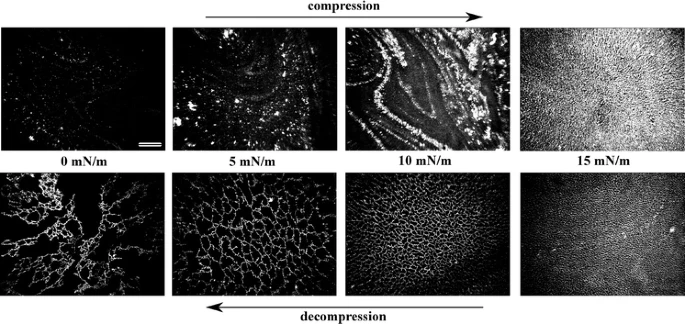
Controlled patterning and formation of nanostructures on surfaces based on self-assembly is a promising area in the field of “bottom-up” nanomaterial engineering. We report formation of net-like structures of gold nanoparticles (Au NPs) in a matrix of liquid crystalline amphiphile 4′-n-octyl-4-cyanobiphenyl at the air–water interface. After initial compression to at least 18 mN m−1, decompression of a Langmuir film of a mixture containing both components results in formation of net-like structures. The average size of a unit cell of the net is easily adjustable by changing the surface pressure during the decompression of the film. The net-like patterns of different, desired average unit cell areas were transferred onto solid substrates (Langmuir–Blodgett method) and investigated with scanning electron microscopy and X-ray reflectivity (XRR). Uniform coverage over large areas was proved. XRR data revealed lifting of the Au NPs from the surface during the formation of the film. A molecular mechanism of formation of the net-like structures is discussed.
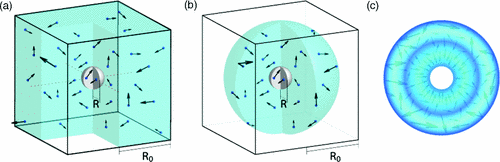
Molecular-dynamics simulations of the Lennard-Jones fluid (up to 107 atoms) are used to analyze the collapse of a nanoscopic bubble. The collapse is triggered by a traveling sound wave that forms a shock wave at the interface. The peak temperature Tmax in the focal point of the collapse is approximately ΣRa0, where Σ is the surface density of energy injected at the boundary of the container of radius R0 and α ≈ 0.4–0.45. For Σ = 1.6 J/m2 and R0 = 51 nm, the shock wave velocity, which is proportional to√Σ, reaches 3400 m/s (4 times the speed of sound in the liquid); the pressure at the interface, which is proportional to Σ, reaches 10 GPa; and Tmax reaches 40 000 K. The Rayleigh-Plesset equation together with the time of the collapse can be used to estimate the pressure at the front of the shock wave.
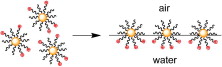
We present a new method to obtain close-packed monolayers composed of noble metal nanoparticles (NP) possessing well-defined permanent charge of either sign. The method is based on the fact that ligands forming the protecting layer exhibit ability to rearrange at the NPs surface. We demonstrate that if the protecting layer is composed of a mixture of hydrophobic and hydrophilic charged ligands in appropriate proportion, the NP exhibits properties of a Janus-type particle with one of the hemispheres hydrophilic and the other hydrophobic. Such amphiphilic NPs self-assemble into a monolayer of well defined surface charge at the air–water interface. Due to strong stabilizing effect of the lateral electrostatic repulsions, such monolayer can be compressed to form close-packed hexagonal structure, and then easily transferred onto a solid substrate with the Langmuir–Blodgett technique.

Galactose oxidase (GalOD) was immobilized on self‐assembled monolayers of thiols on silver and gold surfaces using trans‐stilbene (4,4′‐diisothiocyanate)‐2,2′disulphonic acid (DIDS) as the bridging compound. DIDS is the symmetrical bifunctional reagent that reacted with the amine moiety of the thiol and with primary amino groups of enzyme. The Raman measurement revealed that onto cysteamine‐modified silver and gold electrodes, bands corresponding to the galactose oxidase (about 694, 1076, 1274 cm—1 on Au and 762, 1058, 1274 cm–1 on Ag ) appeared and clearly demonstrated its immobilization onto Au and Ag surfaces. Simultaneously, we have also observed changes in the ratio of trans–gauche conformers of adsorbed cysteamine molecules. Layers revealing high content of trans conformer are transformed into layers composed mainly of cysteamine molecule in gauche conformation after galactose oxidase adsorption. These observations deliver a strong support for enzyme immobilization on cysteamine‐modified gold and silver surfaces. The surface plasmon resonance experiment gave a surface coverage of ~8.4 × 107 g/cm2 for gold electrode modified cysteamine using DIDS chemistry and 1.1 × 107 g/cm2 for the cysteamine only modified gold substrate and demonstrated that galactose oxidase layers immobilized with DIDS coupling reagent are quite stable and cannot be easily removed from the surface by treatment with a buffer solution. The surface plasmon resonance results indicated that in this method, a multilayer of galactose oxidase have been immobilized. Our new method of covalent attachment of enzymes seems to be quite promising as a new way of manufacturing biosensors. Copyright © 2012 John Wiley & Sons, Ltd.

The self-assembly of the tubulin homologue FtsZ at the mid-cell is a critical step in bacterial cell division. We introduce dynamic light scattering (DLS) spectroscopy as a new method to study the polymerization kinetics of FtsZ in solution. Analysis of the DLS data indicates that the FtsZ polymers are remarkably monodisperse in length, independent of the concentrations of GTP, GDP, and FtsZ monomers. Measurements of the diffusion coefficient of the polymers demonstrate that their length is remarkably stable until the free GTP is consumed. We estimated the mean size of the FtsZ polymers within this interval of stable length to be between 9 and 18 monomers. The rates of FtsZ polymerization and depolymerization are likely influenced by the concentration of GDP, as the repeated addition of GTP to FtsZ increased the rate of polymerization and slowed down depolymerization. Increasing the FtsZ concentration did not change the size of FtsZ polymers; however, it increased the rate of the depolymerization reaction by depleting free GTP. Using transmission electron microscopy we observed that FtsZ forms linear polymers in solutions which rapidly convert to large bundles upon contact with surfaces at time scales as short as several seconds. Finally, the best studied small molecule that binds to FtsZ, PC190723, had no stabilizing effect on Caulobacter crescentus FtsZ filaments in vitro, which complements previous studies with Escherichia coli FtsZ and confirms that this class of small molecules binds Gram-negative FtsZ weakly.

We report an innovative application of a true “bottom-up” approach for preparation of functional material. Three consecutive self-assembly steps were utilized for formation of a complex surface enhanced Raman spectroscopy (SERS) platform. First the Langmuir–Blodgett technique was used to deposit gold nanoparticles on a solid substrate. Thus prepared surfaces were afterward used as substrates in the chemical vapor deposition process of gallium nitride (GaN) nanowire growth. On such scaffolding, a third step of material fabrication was performed. Gold microflowers (Au MFs) deposited from solution preferably appeared at the top of the GaN nanowires and not in the cavities in between. The obtained morphology of the final material was controlled at each step of the preparation process to tailor its properties for desired purposes. Prepared surfaces were tested as SERS platforms. The enhancement factor was around 107 in case of p-mercaptobenzoic acid (p-MBA). The platforms were also suitable for biological and biomedical applications. We demonstrated the label free detection of DNA. The substrates gave reproducible SERS spectra both across a single platform and between different platforms. The average spectral correlation coefficients (Γ) was 0.87. Moreover, the obtained material proved to be very stable. The presented complex structure demonstrated therefore had the advantages of the two surface functionalization concepts it comprised: (1) GaN nanowire growth and (2) Au MF deposition, eliminating their major drawbacks. Presented material combined high SERS enhancement factor of Au MFs deposited on a flat surface and good durability of microflowers deposited on a surface completely covered with nanowires, which were almost SERS inactive. The final product provided truly exceptional stability and repeatability of SERS results, maintaining an enhancement factor comparable to the best commercially available platforms.
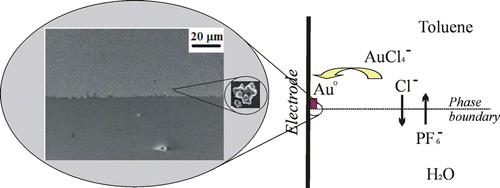
In order to obtain uniform and reproducible surface enhanced Raman spectroscopy (SERS) platforms, a novel method for deposition of well-adhered multifarious gold particles on a tin-doped indium oxide electrode through electrogeneration at an electrode|gold compound in toluene|aqueous-electrolyte three-phase junction was developed. The electrodeposition was carried out both by double-potential-step chronoamperometry with one pulse for nucleation and one for growth of the particles, and by potentiostatic single-potential-step chronoamperometry. Both procedures give angular, multifarious Au particles with a diameter of 150 ± 40 nm. The size of the particles is independent of deposition time, after an initial growth phase, and controlled by the formation of a microemulsion at the three-phase junction. The particles are likely deposited from the microdroplets and their size is determined by the amount of gold salt in a droplet. The mechanism involves electoreduction of tetraoctylammonium tetrachloroaurate at the tin-doped indium oxide electrode followed by ion transfer across the liquid|liquid interface. The Au particles are strongly adhered to the electrode surface. The Au particle covered electrode enhances Raman scattering on the order of 105–106 times for malachite green isothiocyanate. Surface enhanced Raman spectroscopy studies reveal that the reproducibility of the Au particle deposit is excellent both between samples (<15% RSD) and across a single sample (<12% RSD). The obtained nanoparticulate deposit was also demonstrated to show electrocatalytic activity toward dioxygen reduction.
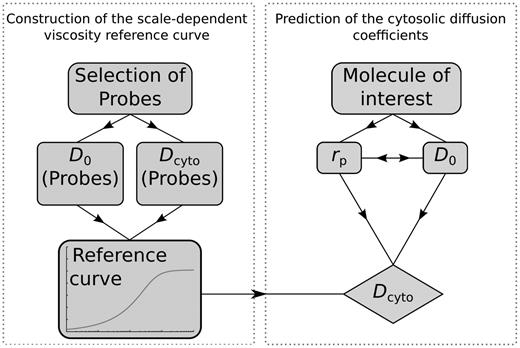
Motivation: Biologistics provides data for quantitative analysis of transport (diffusion) processes and their spatio-temporal correlations in cells. Mobility of proteins is one of the few parameters necessary to describe reaction rates for gene regulation. Although understanding of diffusion-limited biochemical reactions in vivo requires mobility data for the largest possible number of proteins in their native forms, currently, there is no database that would contain the complete information about the diffusion coefficients (DCs) of proteins in a given cell type.
Results: We demonstrate a method for the determination of in vivo DCs for any molecule—regardless of its molecular weight, size and structure—in any type of cell. We exemplify the method with the database of in vivo DC for all proteins (4302 records) from the proteome of K12 strain of Escherichia coli, together with examples of DC of amino acids, sugars, RNA and DNA. The database follows from the scale-dependent viscosity reference curve (sdVRC). Construction of sdVRC for prokaryotic or eukaryotic cell requires ~20 in vivo measurements using techniques such as fluorescence correlation spectroscopy (FCS), fluorescence recovery after photobleaching (FRAP), nuclear magnetic resonance (NMR) or particle tracking. The shape of the sdVRC would be different for each organism, but the mathematical form of the curve remains the same. The presented method has a high predictive power, as the measurements of DCs of several inert, properly chosen probes in a single cell type allows to determine the DCs of thousands of proteins. Additionally, obtained mobility data allow quantitative study of biochemical interactions in vivo.

The fabrication procedure of efficient surface enhanced Raman scattering (SERS) platforms is demonstrated based on reproducibly photo-etched GaN epitaxial layers covered by a thin Au-Ag layer and subjected to partial de-alloying. Using a gold-rich Au57Ag43 alloy (70/30 wt. %), it is possible to preserve about 19 at. % of silver in the layer, even after etching in nitric acid for up to 24 h. A large enhancement of the Raman signal from the test 4-mercaptobenzoic acid molecules attached to such porous Au-Ag metal layer is obtained due to the presence of a high percentage of Ag. For the optimal etching time, in the range of 6–24 h, an enhancement factor (EF) greater than 107 was obtained. The contribution of different features of our SERS platforms such as the size of pores, nano-roughness, and the chemical composition of the metal layer for the EF parameter are critically discussed.
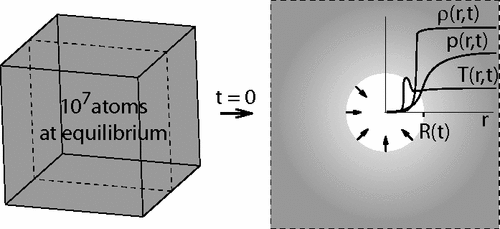
We report large-scale (107 atoms in an 85-nm-wide container) molecular dynamics simulations of collapse of nanoscopic (5–12 nm in diameter) voids in liquid argon. During the collapse the pressure on the liquid side decreases, and this decrease propagates into liquid at the speed of sound. Despite the nonuniform profile of pressure in the liquid the solutions of the Rayleigh-Plesset equation compares well to the measured evolution of the radius of the void and the velocity of the interface. Evaporation of liquid into the void does not affect the dynamics appreciably.
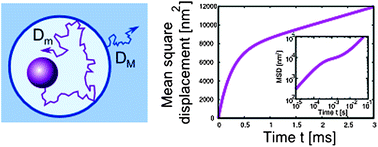
We present a theoretical description of diffusion of a sphere in polymer solution. The depletion layer around the sphere affects its motion and leads to scale-dependent diffusion. We propose the model of walking confined diffusion. Although it is different from anomalous diffusion, we show that the experimental data generated by this process may have features characteristic of anomalous diffusion. We give analytical formulas for the autocorrelation functions describing this type of motion in: i) dynamic light scattering experiments and ii) fluorescence correlation spectroscopy experiments. We compare our results to existing experimental data for polyethylene oxide, fd-virus, and F-actin solutions.
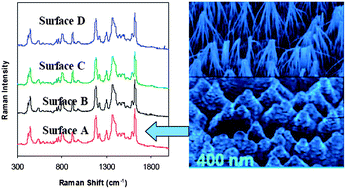
We fabricated a Surface Enhanced Raman Scattering (SERS)-active surface based on photo-etched and Au-coated GaN. The highest enhancement factor (EF) in SERS and high reproducibility of spectra were obtained from surfaces covered with bunched nanopillars which were produced by relatively long defect-selective photo-etching. The surfaces exhibited SERS enhancements of the order of 2.8 × 106 for malachite green isothiocyanate (MGITC) and 2 × 106 for p-mercaptobenzoic acid (PMBA). These SERS enhancement factors were comparable to those of conventional SERS substrates, while the EF for MGITC was two orders of magnitude larger than the corresponding one reported for the SERS platform made on porous GaN. The standard deviation of the relative intensity of the 1180 cm−1 mode of MGITC was less than 5% for 100 randomly distributed locations across a single platform and less than 10% between different platforms. The SERS signal of MGITC at our GaN/Au surface (kept under ambient conditions) was extremely stable. We could not detect any peak shift or appreciable change of intensity even after three months. We used these surfaces to detect biological molecules such as amino acids and bovine serum albumin (BSA) at low concentration and with short detection time. We developed simple and effective cleaning procedures for our substrates. After cleaning, the same substrate could be used multiple times retaining the SERS activity. We are not aware of any other multiply regenerated SERS substrate which provides simultaneously such high stability with high enhancement, good uniformity, and high reproducibility.
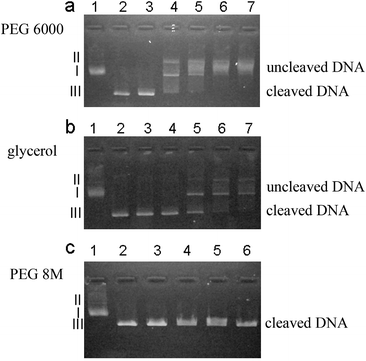
Biochemical reactions in living systems take place in an environment crowded by various macromolecules and ligands. Therefore experimental data obtained in buffer do not reflect in vivo conditions. We have used glycerol poly(ethylene glycol) (PEG) 6000 and PEG 8 M solutions to investigate the influence of the crowded environment on cleavage of plasmid DNA by restriction enzyme HindIII. PEG 6000 solution can effectively slow down the cleavage process. However, neither PEG 8 M solution of the same viscosity as PEG 6000 solution nor glycerol solution of the same concentration as PEG 6000 solution slows the cleavage of DNA appreciably. The viscosity experienced by the biomolecules (here called nano-viscosity) and aggregation induced by the depletion interactions between DNA molecules in polymer solution (PEG 6000) are two factors responsible for slow cleavage of DNA. We have ruled out the change of pH and denaturation of HindIII as possible sources for the effect.
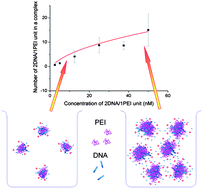
Controlled formation of gene delivery complexes (DNA and a vector, usually a cationic polymer) is one of the key challenges in developing efficient gene delivery systems. The researchers focused their procedures on the ratio of vector to DNA, neglecting the influence of concentration on the complex formation process. In this study we show, by studying the association of polyethylenimine (PEI) and 66-base pair (bp) DNA fragments, that the concentration of the gene delivery system greatly influences the formation of PEI/DNA complexes even at a fixed PEI/DNA ratio. We find that the charge and the size of PEI/DNA complexes are increasing functions of their concentration even in a highly dilute regime of concentrations. The number of PEI/DNA molecules in a complex was calculated from the measured charge and electrophoretic mobility. We established a model, on the basis of Smoluchowski theory, to explain the relation between the concentration and the size of PEI/DNA complexes. We analyzed the structure of the complexes and found out that a large proportion of space in the PEI/DNA complexes is occupied by the solvent. This study indicates that the influence of concentration should be seriously considered in gene delivery studies, since large PEI/DNA complexes can be prepared by scaling up their concentration simultaneously without increasing the dosage of PEI.